Patratele Perfecte Pana La 30

Iar pana la urma nu am reusit nicicum.

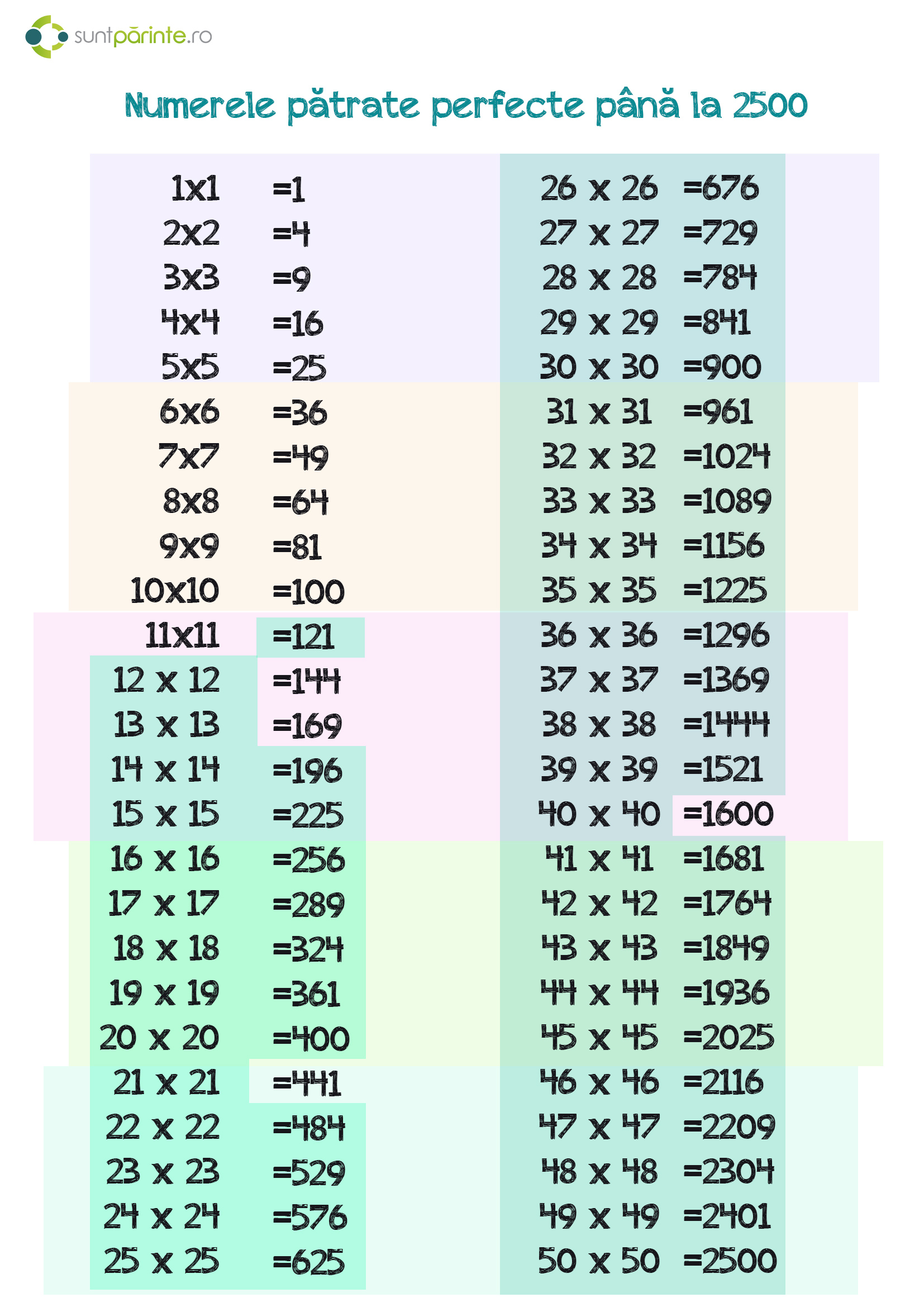
Patratele perfecte pana la 30. în matematică un pătrat perfect este un număr întreg care este pătratul unui alt număr. Pentru ca imi trebuie la scoala si profesoara a zis sa le luam de pe net si eu nu gasesc nici unde ma puteti ajuta va rog. Lista cu patratele perfecte pana la 30 4589126. Arătaţi că nu există pătrate perfecte de forma 5 3k k n.

Programul contine cate 20 30 de minute de alergat la un ritm moderat dupa cateva din antrenamentele de baza. In plus iata si cateva definitii si informatii care il pot ajuta pe copil sa inteleaga mai bine patratele perfecte. Verificaţi dacă cel puţin trei din divizorii lui 72 sunt pătrate perfecte. B demonstraţi că nu există pătrate perfecte de forma 10 2n 32.

Numele de pătrat provine de la denumirea figurii omonime. Dau funda 1 1 2 4 3 9 4 16 5 25 6 36 7 49 8 64 9 81 10 100 11 121 12 144 13 169 14 196 15 225 16 256 17 289 18 324 19 361 20 400 21 441 22 484 23 529 24 576. Aratati ca pentru orice exista x si y patrate perfecte astfel incat gm 2 1986 solutie. Trimisă pe 13 martie.

Plsssss daca puteti sa raspundeti un pic mai repede. Acum poti obtine acces instant la antrenamentul 6 patratele in 24 de zile pentru o singura plata 100 sigura de doar 100 ron. Imi puteti spune si mie care sunt patratele perfecte. Cum si 144 este patrat perfect deducem ca numarul cerut este chiar 441.

Notația obișnuită pentru pătratul unui număr n nu este produsul n n ci puterea n 2 citită n la pătrat sau n pătrat. Scrieţi două numere naturale pătrate perfecte divizibile cu 13. 900 30 30 961 31 31 1024 32 32 1089 33 33 1156 34 34 1225 35 35 1296 36 36 1369 37 37 1444 38 38 1521 39 39 1600 40 40. Vroiam sa spun pana la 100000.

Dau funda o3. Patratele perfecte ale numerelor mai mici ca 30 categories. Mai sus poti gasi o astfel de lista pana la 2500 pe care o poti salva pe calculator click dreapta si save as salveaza ca si o poti printa. Pătratul perfect este orice număr care se poate scrie ca puterea a doua a altui număr natural.

Dintre patratele perfecte de trei cifre care incep cu una dintre aceste cifre si care au cifra unitatilor egala cu cea a zecilor putem alege doar pe 441.